数値予報モデルの出力値や一部の解析値など、格子状の分布を持つ気象データは「GPV」と呼ばれます。
今回はGPVの基礎知識を解説した上で、「最も近い格子点の値を抽出し、予報値として利用する」という方法をご紹介します。
特に、これから気象データを扱ってみようと考えている方にとって入り口となるポイントをまとめました。
- この記事のポイント
- GPVは格子点上の気象要素などの値を表す気象データである。
- GPVは格子点領域の代表値であるということを理解する。
- GPVを利用する際は、仕様書等から格子系を確認する。
- この記事のゴール
- 最も近い格子点の値を抽出し、予報値として利用する。
GPV(Grid Point Value)
GPVとは、「格子点値」という意味を持つ「Grid Point Value」の略です。
設定された格子点上の気象要素などの値を表す気象データです。
一般的には、数値予報モデルの出力結果(数値予報モデルGPVと言います)を意味することが多いです。
気象庁の全球数値予報モデルの出力値は「GSM-GPV」、メソ数値予報モデルは「MSM-GPV」と呼ばれます。
もう少し意味広げると、レーダーや解析雨量のような解析値もGPVに含まれます。
また、必ずしも等間隔の格子系である必要はありません。
ランベルト図法のような特殊な格子系であっても、各格子点の物理量を規則的に表現しているデータであれば、GPVと呼ぶことができます。
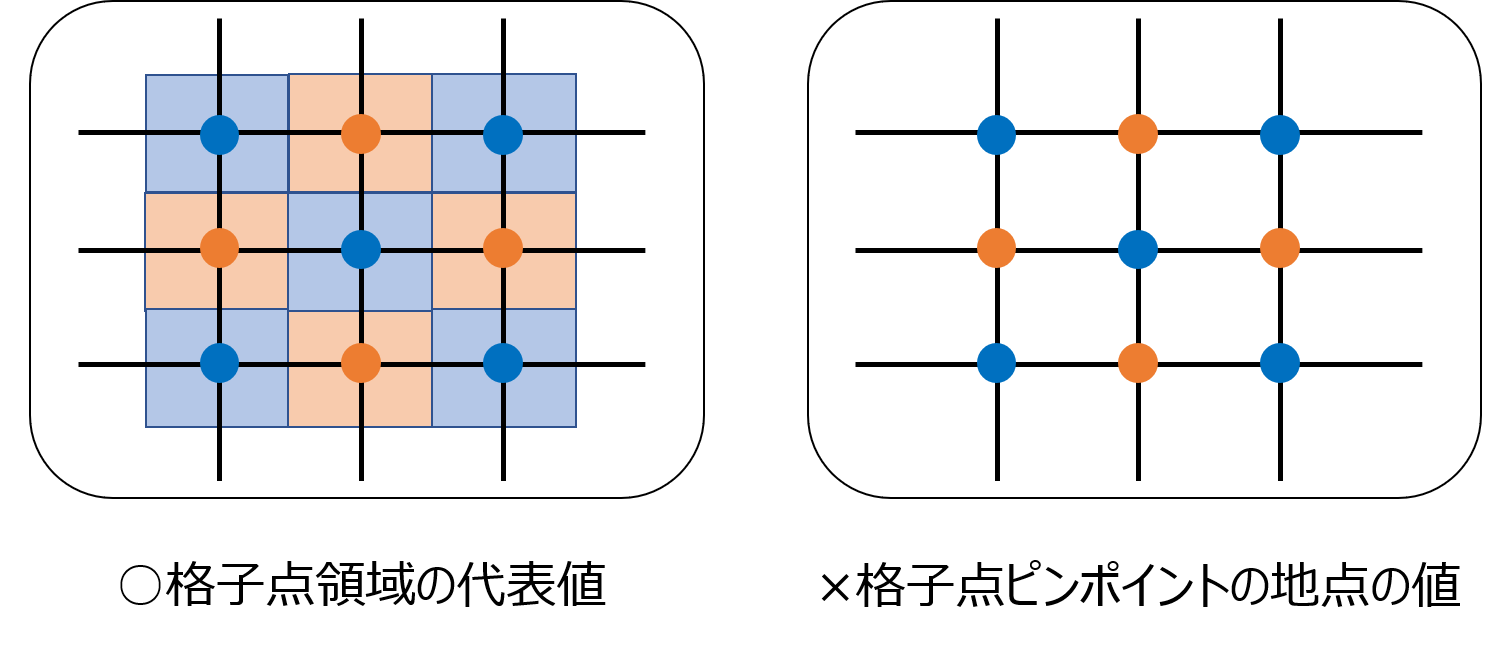
GPVは格子点領域の代表値
誤解されることが多いのですが、GPVとは「格子点領域の代表値」であり、「その格子点ピンポイントの地点の値」ではありません。
GPVの格子系を距離に換算すると「1kmメッシュ」「5kmメッシュ」「20㎞メッシュ」などと表現できます。
一般的に「細かいメッシュのデータが必要」という要望を多くお聞きします。
しかし、粗いメッシュであっても、領域内の全ての地点を対象地点として扱うことができます。
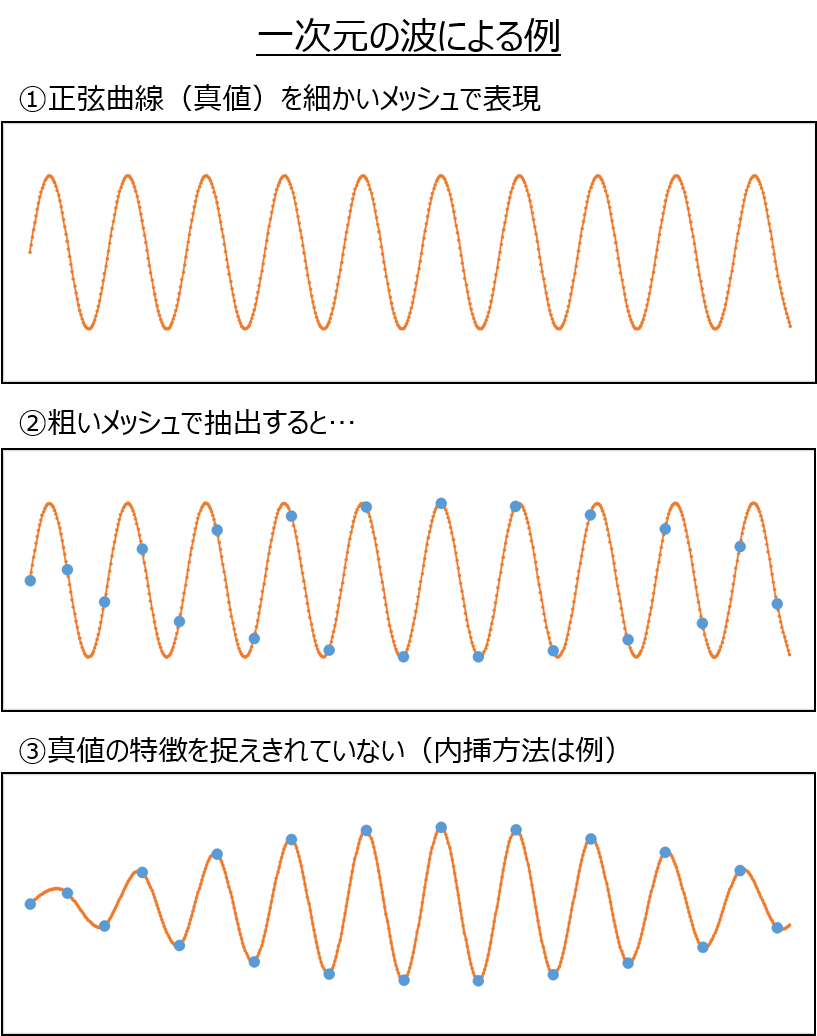
ただし、GPVが現実の現象をどれだけ表現できているかには注意が必要です。
数値予報モデルが表現できる現象に限界があることや、モデルの地形や標高が現実と一致しないことなどが原因として挙げられます。
細かいメッシュのデータの方が精度が良いと度々いわれる所以は、スケールの小さな現象を表現できる可能性が高いという点にあります。
最も近い格子点を利用する方法
先ほど述べたGPVの特性から、予報地点の値として最も近い格子点の値を扱うという選択肢があります。
以下、その手順を紹介します。
今回は、grib2形式等のバイナリデータやテキスト変換したCSV等を扱うことができる前提で進めます。
別の記事(GRIB2形式データを処理するプログラムwgrib2(入門編))なども参照下さい。
格子系の仕様を確認する
GPVに限らず、気象データを扱う際は、まずは仕様書等の情報を確認します。
例として、水平方向の格子系が以下のような仕様のGPVデータを考えてみましょう。
| 要素 | 内容 |
|---|---|
| データ領域 | 北緯20度~50度、東経120度~150度 |
| 水平分解能 | 緯度方向5度、経度方向6度 |
| 格子点数 | 緯度方向7、経度方向6 |
地図に描画してみると、一目で把握できます。
下図のような日本付近の等緯度経度の格子系になり、縦線と横線の交点がそれぞれ格子点になります。
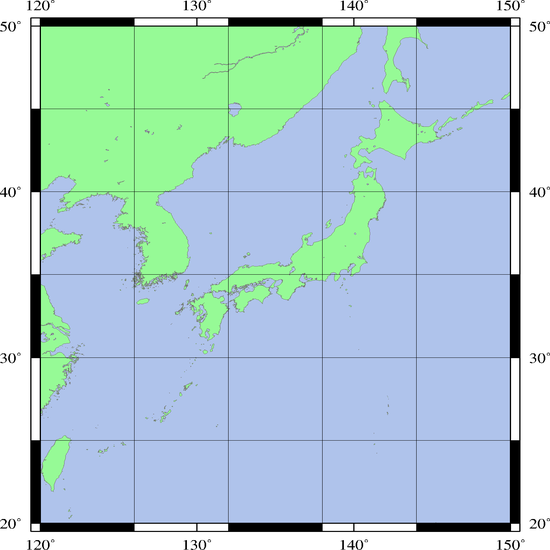
※描画にはGMT(Generic Mapping Tools)というソフトウェアを利用しました。
等緯度経度の格子系の場合、南北・東西端の緯度経度、分解能、格子点数は整合性が取れています。
南北方向:20+5×(7-1)=50
東西方向:120+6×(6-1)=150
といった確認もしておくと、理解が深まるかと思います。
最も近い格子点を抽出する方法
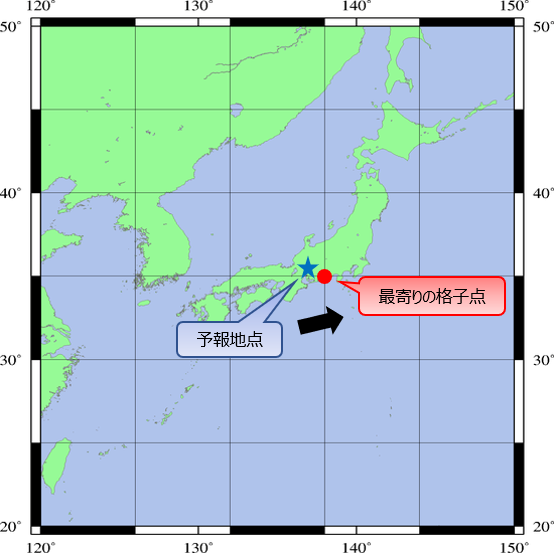
格子系の情報を用いて、予報地点から一番近い格子点を抽出します。
下図のように、青い星で示した予報地点に最も近い格子点(赤い丸)を判定するイメージです。
私はFortranを用いてデータを処理することが多いですので、前述の格子系を例に、ある地点(緯度・経度が既知)に最も近い格子点を抽出するサンプルプログラムを紹介します。
プログラム内のコメント【要点】の計算式を参考にして下さい。
格子系の情報を基に、領域の端と対象地点の緯度・経度の差を取り、水平分解能で割ることで、何番目の格子点が最も近いかを求めています。
integer i,j
! 格子系を定義する
integer imax,jmax ! 東西・南北方向の格子点数
parameter (imax=6,jmax=7)
real ilat,elat,ilon,elon ! 南・北・西・東端の緯度・経度
parameter (ilat=20.0,elat=50.0,ilon=120.0,elon=150.0)
real dlat,dlon ! 南北・東西方向の分解能
parameter (dlat=5.0,dlon=6.0)
! ある時刻における物理量の配列
real array(imax,jmax)
! 予報地点の緯度・経度
real lat,lon
! 予報地点の物理量
real var
!!! 処理手順
! 準備1:予報値を配列arrayに格納する
! 準備2:対象地点の緯度・経度を変数lat,lonに当てはめる
! 【要点】東西方向の格子点番号
i = nint((lon-ilon)/dlon)+1
! 【要点】南北方向の格子点番号
j = nint((lat-ilat)/dlat)+1
! [不具合確認]格子点番号が領域の範囲内であることを確認する
if(i.lt.1 .or. i.gt.imax .or. j.lt.1 .or. j.gt.jmax) then
print*,'!!! out of region !!!'
call exit(255) ! 異常終了として扱う
endif
! 算出した格子点番号を用いて、予報地点の物理量を設定
var = array(i,j)
! [補足]配列arrayをそのまま用いて、array(i,j)で後続処理を行っても良い
!!! 以降、任意の処理を行う
end
まとめ
GPVの基礎を踏まえ、最も近い格子点値を予報値として利用する方法をご紹介しました。
格子点データはこちらをご覧下さい。
今回は各種GPVで利用できる汎用的な内容ですが、今後は実際のデータを扱った具体例も紹介していこうと考えています。
この記事を書いた人
K.Enohara
学生時代に地球科学の魅力に惹かれ、気候変動を研究テーマに海洋物理学を専攻。
本サービスでは、気象庁データのフォーマット変換システムや、過去データ提供システムの構築、プレミアム気象データのうち天気予測データや指数予報などの開発を担当。
音楽・野球・ツーリング・将棋など比較的多趣味。気象予報士。

